II.8.3.2.3 Choix des directions à partir des directions de référence.

Les directions des fonctions de base sont prises de la façon suivante.

i) Constantes.

Tous les éléments ont les mêmes directions de propagation.

ii) Variantes d'un élément à l'autre.

A partir des positions de référence des ondes planes on effectue dans un repère terrestre une rotation en latitude d'angle $\phi$ entre $-\pi/2$ et $+\pi/2$ puis on effectue une rotation en longitude d'angle $\theta$ entre $-\pi$ et $+\pi$. La première étape consiste à multiplier les coordonnées du premier vecteur de la base canonique par la matrice

$$\left[ \begin{array}{ccc} \cos{(\phi)} & 0 & \sin{(\phi)} \\... ... -\sin{(\phi)} & 0 & \cos{(\phi)} \\ \end{array}\right] \ ,$$

la deuxième étape consiste à multiplier par la matrice

$$\left[ \begin{array}{ccc} \cos{(\theta)} & \sin{(\theta)} & ... ... & \cos{(\theta)} & 0 \\ 0 & 0 & 1 \\ \end{array}\right] \ .$$

Les lois de répartition des variables aléatoires $\phi$ et $\theta$ peuvent être des deux formes suivantes:

1. Loi uniforme en 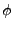$\phi$ : cela introduit une anisotropie polaire sur la loi de répartition de la fonction de base de coordonnées
   
   $$\left( \begin{array}{ccc} \cos{(\theta)} \cos{(\phi)} & -\sin{(\theta)} \cos{(\phi)} & -\sin{(\phi)} \end{array} \right)$$
   
   
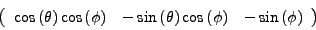
   Se reporter à la figure II.8.3 b) donnant une idée de cette anisotropie polaire parasite. La loi de répartition, en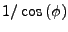 $1/\cos{(\phi)}$, est singulière aux pôles.
2. Loi de probabilité sur la variable aléatoire de latitude 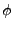$\phi$ en $\cos{(\phi)}$ : Cela supprime l'anisotropie polaire sur la loi de répartition de la fonction de base citée ci-dessus. On constate, sur la figure II.8.3 a), la répartition uniforme sur la sphère de cette fonction de base. C'est cette loi que nous avons prise. Le lecteur vérifiera que les changements de variables aléatoires C¹ difféomorphismes,
   
   $$\left\{ \null\,\vcenter{\openup\jot \let\\ =\@ \ialign{\str... ...beta) \cr & [0,1] \rightarrow [-\pi,\pi] \cr \crcr}}\, \right.$$
   
   
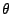   appliqués à des paramètres $\alpha$ et $\beta$ suivant des lois de répartition uniformes sur le segment [0,1], donnent bien une loi uniforme sur $\theta$ et une loi de probabilité sur 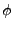$\phi$ en $\cos{(\phi)}$, donc une loi de répartition uniforme sur la sphère.

Figure II.8.3: Lois de répartition selon le choix des variables aléatoires

a)	b)