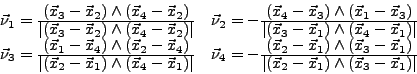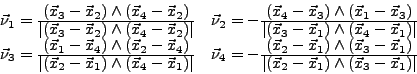III.E.2.0.1 Notations.

On considère le tétraèdre (numéroté par l'indice k que l'on omet pour ne pas alourdir les notations) défini par

1. les sommets 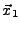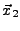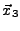$\vec{x}_1$, $\vec{x}_2$, $\vec{x}_3$ et $\vec{x}_4$.
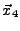2. les arêtes 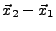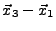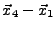$\vec{x}_2-\vec{x}_1$, $\vec{x}_3-\vec{x}_1$, $\vec{x}_4-\vec{x}_1$ qui forment un trièdre orienté positivement
3. les faces numérotées (1,2,3,4) correspondant respectivement aux triangles 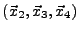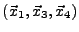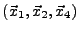$(\vec{x}_2,\vec{x}_3,\vec{x}_4)$, $(\vec{x}_1,\vec{x}_3,\vec{x}_4)$, $(\vec{x}_1,\vec{x}_2,\vec{x}_4)$ et $(\vec{x}_1,\vec{x}_2,\vec{x}_3)$,
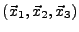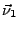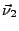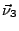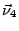4. les normales externes (notées $\vec{\nu}_1$, $\vec{\nu}_2$, $\vec{\nu}_3$ et $\vec{\nu}_4$) aux faces (1,2,3,4) sont définies par:
   

   $$\begin{array}{lr} \vec{\nu}_1 = \frac{\displaystyle (\vec{x}... ...2-\vec{x}_1) \wedge (\vec{x}_3-\vec{x}_1)\vert} \\ \end{array}$$ (III.E.14)

   
   
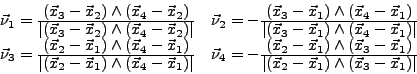   ou
   

   $$% \begin{array}{lr} \vec{\nu}_1 = \frac{\displaystyle (\vec{x... ...2-\vec{x}_1) \wedge (\vec{x}_3-\vec{x}_1)\vert} \\ \end{array}$$ (III.E.15)

   
   

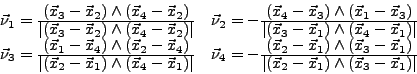5. les quatre surfaces notées S₁,S₂,S₃,S₄, la plus grande de ces quatre surfaces sera simplement notée S,
6. le volume noté V.