




suivant: II.8.3.2.2 Exemples.
monter: II.8.3.2 Choix des directions de propagation sur
précédent: II.8.3.2 Choix des directions de propagation sur
Table des matières
Index
II.8.3.2.1 Choix des directions de propagation de référence.
Nous donnons des directions de référence des fonctions de base qui serviront dans le choix final des directions. Nous avons choisi de prendre en priorité des directions équiréparties, sinon
le découpage Sn de la sphère, sinon des directions qui nous semblent assez bien découper la sphère, et enfin nous proposons un algorithme général de choix des directions, algorithme
qu'il serait intéressant d'améliorer à l'avenir.
- i) Equiréparties.
- Dans certains cas, nous avons pu choisir des directions équiréparties dans l'espace. Pour trois fonctions de base les directions forment un triangle équilatéral dans le plan équatorial.
Pour quatre, un tétraèdre régulier. Pour six, deux tétraèdres réguliers assemblés par une face. Pour huit, un cube. Pour douze on a pris les n
 uds de l'icosaèdre.
uds de l'icosaèdre.
- ii) Découpage Sn de la sphère en n(n+2) directions.
- Ce découpage est bien connu des neutroniciens. Il consiste à effectuer un découpage de l'espace des phases
 où la quantité
où la quantité  est liée à l'angle
est liée à l'angle 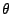 par
par
 . Les angles
. Les angles  donnent les coordonnées d'un point de la sphère unité dans un repère cartésien
par
donnent les coordonnées d'un point de la sphère unité dans un repère cartésien
par
 . L'espace des phases
. L'espace des phases  est donc le quadrilatère
est donc le quadrilatère
![$[0,\pi]\times[-1,+1]$](img744.gif) . L'avantage de cette répartition est
qu'elle découpe l'espace des phases en quadrangles d'aires égales. Les neutroniciens l'utilisent pour des propriétés de quadratures
des moments du vecteur courant
. L'avantage de cette répartition est
qu'elle découpe l'espace des phases en quadrangles d'aires égales. Les neutroniciens l'utilisent pour des propriétés de quadratures
des moments du vecteur courant
 défini par
défini par
Ce découpage nous a semblé assez bien ``équiréparti'' au sens qu'il produit une partition quadrangulaire de la sphère unité qui est assez régulière. Nous renvoyons aux ouvrages
de neutronique qui utilisent ce découpage pour des explications plus précises, nous ne donnons ici que le tableau (II.8.1) de construction des directions
Vm,l de la demi-sphère unité. L'indice m correspond à une latitude, l'indice l à une longitude.
Tableau II.8.1:
Récapitulatif du découpage Sn.
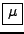 |
 |
 |
 |
 |
 |
 |
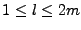 |
 |
 |
 |
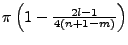 |
La figure (II.8.1) représente le découpage pour n=16 (image Guillaume Pottier). Les directions sont proches des barycentres des quadrangles.
Figure II.8.1:
Découpage Sn=16 de la sphère unité.
|
|
- iii) Construction ``à la main''.
- Pour des nombres différents de fonctions de base, nous avons pris dans certains cas des directions construites à la main. Ainsi, pour cinq fonctions de base, nous avons pris les trois fonctions
équiréparties du cas ci-dessus, puis nous avons rajouté les deux pôles. Pour sept fonctions nous avons pris celles du tétraèdre régulier plus celles du plan équatorial de façon
à former, vu de dessus, un point à l'origine et deux triangles obtenus l'un de l'autre par homothétie et symétrie par rapport à l'origine. Pour neuf fonctions nous avons pris les trois
directions du plan équatorial auxquelles nous avons rajouté trois fonctions dans un plan parallèle à une latitude de 45 degrés dans un repère terrestre. Ces directions forment un
triangle équilatéral dans leur plan et leur projection sur le plan équatorial est un triangle aux côtés parallèles aux côtés du triangle du plan équatorial, mais par les faces
les plus éloignées. Les trois dernières directions sont symétriques par rapport au plan équatorial. Enfin pour vingt fonctions nous avons pris les n
 uds du dodécahèdre sachant
qu'ils ne forment pas un maillage équiréparti de la sphère.
uds du dodécahèdre sachant
qu'ils ne forment pas un maillage équiréparti de la sphère.
- iv) Génération automatique non équirépartie.
- Pour d'autres nombres de fonctions de base nous construisons les directions par un algorithme qui, asymptotiquement, donne des directions équiréparties. Nous prenons le pôle Nord et le
pôle Sud puis un nombre N pour l'instant inconnu de fonctions de base aux directions équiréparties dans le plan équatorial. A une latitude d'angle
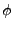 égal à (N/4)*4
(division entière) fois l'angle entre deux directions consécutives du plan équatorial nous prenons un nombre
égal à (N/4)*4
(division entière) fois l'angle entre deux directions consécutives du plan équatorial nous prenons un nombre
![$[N*\cos{(\phi)}]$](img761.gif) (rappelons que
(rappelons que ![$[\alpha]$](img50.gif) est le symbole partie
entière de
est le symbole partie
entière de  ) de directions équiréparties dans leur plan. Cet algorithme permet une anisotropie polaire faible par rapport à un simple maillage quadrangulaire en latitude-longitude, pôles exclus.
En même temps que nous construisons les directions de l'hémisphère Nord nous construisons les directions symétriques de l'hémisphère Sud. Nous ne tombons pas forcément sur exactement le
bon nombre de fonctions de base. Nous calculons d'abord le nombre N donnant le plus petit nombre de directions construites par l'algorithme supérieur au nombre de fonctions de bases demandé.
Nous stoppons ensuite le procédé lorsque le nombre demandé est atteint ce qui peut créer une légère anisotropie supplémentaire aux pôles. Par exemple pour 17 fonctions de base demandées
l'algorithme est prêt à en constituer 20. Pour 40 l'algorithme serait pleinement efficace pour 44. A la place de 90 fonctions il serait mieux d'en demander 95, pour 200 ce serait 203 et
800 ce serait 814. La figure II.8.2 pour 300 directions est typique: en coupe équatoriale nous observons un ``trou'' aux deux pôles dans les répartitions des
directions. C'est le problème de la couche d'ozone...
) de directions équiréparties dans leur plan. Cet algorithme permet une anisotropie polaire faible par rapport à un simple maillage quadrangulaire en latitude-longitude, pôles exclus.
En même temps que nous construisons les directions de l'hémisphère Nord nous construisons les directions symétriques de l'hémisphère Sud. Nous ne tombons pas forcément sur exactement le
bon nombre de fonctions de base. Nous calculons d'abord le nombre N donnant le plus petit nombre de directions construites par l'algorithme supérieur au nombre de fonctions de bases demandé.
Nous stoppons ensuite le procédé lorsque le nombre demandé est atteint ce qui peut créer une légère anisotropie supplémentaire aux pôles. Par exemple pour 17 fonctions de base demandées
l'algorithme est prêt à en constituer 20. Pour 40 l'algorithme serait pleinement efficace pour 44. A la place de 90 fonctions il serait mieux d'en demander 95, pour 200 ce serait 203 et
800 ce serait 814. La figure II.8.2 pour 300 directions est typique: en coupe équatoriale nous observons un ``trou'' aux deux pôles dans les répartitions des
directions. C'est le problème de la couche d'ozone...





suivant: II.8.3.2.2 Exemples.
monter: II.8.3.2 Choix des directions de propagation sur
précédent: II.8.3.2 Choix des directions de propagation sur
Table des matières
Index
Cessenat Olivier
2007-04-21
![\includegraphics[width=9.5cm,height=9.5cm]{maxdirfig2.ps}](img759.gif)